Conditional Probability

Conditional Probability

The notation P(F|E) is read "the probability of F given E" and represent the probability that event F occurs, given that event E has already occurred.

Example 1

Consider the experiment where two cards are drawn without replacement. (Without replacement means one is drawn and then the second is drawn without putting the first one back.) Define events E and F this way:

E = the first card drawn is a King

F = the second card drawn is a King

Find P(F|E).

ANSWER

P(F|E) is the probability that the second card is a king given if the first card drawn was a king. In that case, there will be 3 kings left out of 51 cards, so

P(F|E) = 3/51

It can be helpful again to look at a Venn diagram to illustrate the idea. Let's look at this one that we used back in section 5.2.

Example 2

Find P(E|F).

ANSWER

OK, this is a little trickier. P(E|F) is the probability that event E occurs given that event F has already occurred. Let's change the image a bit. Since F has occurred, we can focus on just those "outcomes" in F.

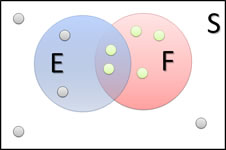
And then of those, we want the probability that the "outcome" is in E. Since there are 2 of those in E, and 5 total,

P(E|F) = 2/5.

One more example.

Example 3

Let's consider a survey given to 52 students in a Basic Algebra course at ECC, with the following responses to the statement "I enjoy math."

	Strongly Agree	Agree	Neutral	Disagree	Strongly Disagree	Total
Male	6	10	3	0	0	19
Female	8	14	7	4	0	33
Total	14	24	10	4	0	52

What is the probability that a student enjoys math (Agree or Strongly Agree) given that the student is a female?

ANSWER

There are 33 female students total. Of those, 22 responded that they enjoyed math, so...

P(enjoys math | female) = 22/33 = 2/3