Counting Techniques

Counting

An efficient way of counting is necessary to handle large masses of statistical data (e.g. the level of inventory at the end of a given month, or the number of production runs on a given machine in a 24 hour period, etc.), and for an understanding of probability.

In this section, we shall develop a few counting techniques. Such techniques will enable us to count the following, without having to list all of the items:

• the number of ways,
• the number of samples, or
• the number of outcomes.

The Multiplication Rule of Counting

Let's suppose you're preparing for a wedding, and you need to pick out tuxedos for the groomsmen. Men's Tuxedo Warehouse has a Build-A-Tux feature which allows you to look at certain combinations and build your tuxedo online. Let's suppose you have the components narrowed down to two jackets, two vest and tie combinations, and three shirt colors. How many total combinations might there be?

A good way to help understand this type of situation is something called a tree diagram. We begin with the jacket choices, and then each jacket "branches" out into the two vest and tie combinations, and then each of those then "branches" out into the three shirt combinations. It might look something like this:

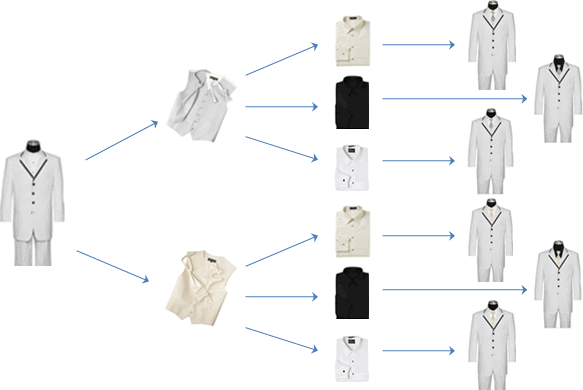
In total, it looks like we have 12 possible combinations of jackets, vests, and shirts. (Of course, some may not fit your fashion sense, but that's another question all-together...)

Isn't there an easier way to do this? Why yes, there is! Think of it this way, for each jacket choice, there are two vest and tie choices. That gives us 4 total jacket and vest/tie combinations. Then, for each of those, there are three shirt choices, giving us a total of 12.

In general, we multiply the number of ways to make each choice, so...

total number of outfits = (number of jackets)•(number of vest/ties)•(number of shirts)

That leads us to the Multiplication Rule of Counting:

Multiplication Rule of Counting

f a task consists of a sequence of choices in which there are p ways to make the first choice, q ways to make the second, etc., then the task can be done in

p•q•r•...

different ways.

Let's try some examples.

Example 1

How many 7-character license plates are possible if the first three characters must be letters, the last four must be digits 0-9, and repeated characters are allowed?

The total number of license plates would be:

(# choices for 1st character)•(# choices for 2nd)•etc..

= 26•26•26•10•10•10•10 = 175,760,000

Video

Permutations

Let’s start with permutations, or all possible ways of doing something. We’re using the fancy-pants term “permutation”, so we’re going to care about every last detail, including the order of items. Let’s say we have 8 people:

1. Alice
2. Bob
3. Charlie
4. David
5. Eve
6. Frank
7. George
8. Horatio

How many ways can we pick a Gold, Silver, and Bronze medal for “Best friend in the world”?

We’re going to use permutations since the order we hand out these medals matter. Here’s how it breaks down:

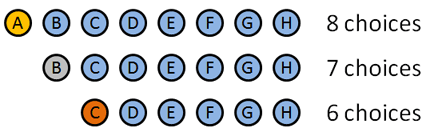
• Gold medal: 8 choices: A B C D E F G H (Clever how I made the names match up with letters, eh?). Let’s say A wins the Gold.
• Silver medal: 7 choices: B C D E F G H. Let’s say B wins the silver.
• Bronze medal: 6 choices: C D E F G H. Let’s say… C wins the bronze.

We picked certain people to win, but the details don’t matter: we had 8 choices at first, then 7, then 6. The total number of options was 8 * 7 * 6 = 336.

Let’s look at the details. We had to order 3 people out of 8. To do this, we started with all options (8) then took them away one at a time (7, then 6) until we ran out of medals.

We know the factorial is: 

Unfortunately, that does too much! We only want 8 * 7 * 6. How can we “stop” the factorial at 5?

This is where permutations get cool: notice how we want to get rid of 5*4*3*2*1. What’s another name for this? 5 factorial!

So, if we do 8!/5! we get:

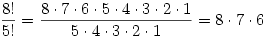
And why did we use the number 5? Because it was left over after we picked 3 medals from 8. So, a better way to write this would be:

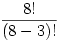
where 8!/(8-3)! is just a fancy way of saying “Use the first 3 numbers of 8!”. If we have n items total and want to pick k in a certain order, we get:

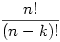 just means “Use the first k numbers of n!”

And this is the fancy permutation formula: You have n items and want to find the number of ways k items can be ordered:

As a side note, your text uses the notation _nP_k rather than Kalid's P(n,k). I've seen both used, though the later tends to be more prevalent in higher-level math classes. We'll stick with the textbook version, just to be consistent.

Permutations of n Distinct Objects Taken r at a Time

The number of arrangements of r objects chosen from n objects in which

1. the n objects are distinct,
2. repeats are not allowed,
3. order matters,

is given by the formula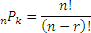 

Video

Combinations

Combinations are easy going. Order doesn’t matter. You can mix it up and it looks the same. Let’s say I’m a cheapskate and can’t afford separate Gold, Silver and Bronze medals. In fact, I can only afford empty tin cans.

How many ways can I give 3 tin cans to 8 people?

Well, in this case, the order we pick people doesn’t matter. If I give a can to Alice, Bob and then Charlie, it’s the same as giving to Charlie, Alice and then Bob. Either way, they’re going to be equally disappointed.

This raises and interesting point — we’ve got some redundancies here. Alice Bob Charlie = Charlie Bob Alice. For a moment, let’s just figure out how many ways we can rearrange 3 people.

Well, we have 3 choices for the first person, 2 for the second, and only 1 for the last. So we have 3 * 2 * 1 ways to re-arrange 3 people.

Wait a minute… this is looking a bit like a permutation! You tricked me!

Indeed I did. If you have N people and you want to know how many arrangements there are for all of them, it’s just N factorial or N!

So, if we have 3 tin cans to give away, there are 3! or 6 variations for every choice we pick. If we want to figure out how many combinations we have, we just create all the permutations and divide by all the redundancies. In our case, we get 336 permutations (from above), and we divide by the 6 redundancies for each permutation and get 336/6 = 56.

The general formula is

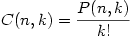
which means “Find all the ways to pick k people from n, and divide by the k! variants”. Writing this out, we get our combination formula, or the number of ways to combine k items from a set of n:

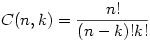
As a side note, your text uses the notation _nC_k rather than Kalid's C(n,k). As with permutations, we'll stick with the textbook version, just to be consistent.

Combinations of n Distinct Objects Taken r at a Time

The number of arrangements of n objects using r≤n of them, in which

1. the n objects are distinct,
2. repeats are not allowed,
3. order does not matter,

is given by the formula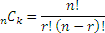 

Example

In how many ways could the letters in the word STATISTICS be rearranged?

The answer is a little tricky. Think of the rearranged words as places for letters to go. Something like this:

In STATISTICS, we have the following letters:

3 S's
3 T's
2 I's
1 A
1 C

We can't really say that there are 4 choices for the first letter and proceed from there, since the number of choices for the second letter depend on which letter was chosen for the first.

Instead, we choose the spots for each of the letters. First, pick 3 of the 10 spots for the S's. We can do that in ₁₀C₃ ways. Then pick 3 spots for the 3 T's. We can do that in ₇C₃ ways. Similarly, we can pick the spots for the I's, the A, and the C in ₄C₂, ₂C₁, and ₁C₁ ways, respectively. In total, that means we rearrange the letters in:

₁₀C₃•₇C₃•₄C₂•₂C₁•₁C₁ ways

It may just be me, that is really messy. Oddly enough, writing out the combinations reveals a nice way to simplify it:

10!	•	7!	•	4!	•	2!	•	1!	=	10!
7!•3!		4!•3!		2!•2!		1!•1!		1!•0!		3!•3!•2!•1!•1!