Mean, Variance, Standard Deviation and Expected Value

Expected Value of a Random Variable

Let X represent a discrete random variable with the probability distribution function P(X). Then the expected value of X denoted by E(X), or μ, is defined as:

E(X) = μ = Σ (x_i × P(x_i))

To calculate this, we multiply each possible value of the variable by its probability, then add the results.

Σ (x_i × P(x_i)) = { x₁ × P(x₁)} + { x₂ × P(x₂)} + { x₃ × P(x₃)} + ...

$\displaystyle{E}{\left({X}\right)}$ is also called the mean of the probability distribution.

Example 4

In Example 1 above, we had an experiment where we drew $\displaystyle{2}$ balls from an urn containing $\displaystyle{4}$ red and $\displaystyle{6}$ black balls. What is the expected number of red balls?

ANSWER

We already worked out the probabilities before:

Possible Outcome	RR	RB	BR	BB
xi	$\displaystyle{2}$	$\displaystyle{1}$	$\displaystyle{1}$	$\displaystyle{0}$
P(xi)	$\displaystyle\frac{2}{{15}}$	$\displaystyle\frac{4}{{15}}$	$\displaystyle\frac{4}{{15}}$	$\displaystyle\frac{1}{{3}}$

$\displaystyle{E}{\left({X}\right)}=\sum{\left\lbrace{x}_{{i}}\cdot{P}{\left({x}_{{i}}\right)}\right\rbrace}$

$\displaystyle={2}\times\frac{2}{{15}}+{1}\times\frac{4}{{15}}+{1}\times\frac{4}{{15}}+{0}\times\frac{1}{{3}}$

$\displaystyle=\frac{4}{{5}}$

$\displaystyle={0.8}$

This means that if we performed this experiment 1000 times, we would expect to get 800 red balls.

Variance of a Random Variable

Let X represent a discrete random variable with probability distribution function $\displaystyle{P}{\left({X}\right)}$. The variance of X denoted by $\displaystyle{V}{\left({X}\right)}$ or σ² is defined as:

V(X) = σ² = Σ[{X − E(X)}² × P(X) ]

Since μ = E(X), (or the average value), we could also write this as:

V(X) = σ² = Σ[{X − μ}² × P(X) ]

Another way of calculating the variance is:

V(X) = σ² = E(X²) − [E(X)]²

Standard Deviation of the Probability Distribution

$\displaystyle\sigma=\sqrt{{{V}{\left({X}\right)}}}$ is called the standard deviation of the probability distribution. The standard deviation is a number which describes the spread of the distribution. Small standard deviation means small spread, large standard deviation means large spread.

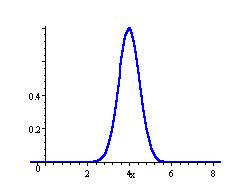
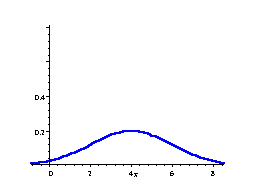
In the following 3 distributions, we have the same mean (μ = 4), but the standard deviation becomes bigger, meaning the spread of scores is greater.

Normal Curve
μ = 4, σ = 0.5

Normal Curve
μ = 4, σ = 1

Normal Curve
μ = 4, σ = 2

The area under each curve is $\displaystyle{1}$.