Sine, cosine, and tangent

Right Triangle

Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle.

Before getting stuck into the functions, it helps to give a name to each side of a right triangle: 

• "Opposite" is opposite to the angle θ
• "Adjacent" is adjacent (next to) to the angle θ
• "Hypotenuse" is the long one

Adjacent is always next to the angle
And Opposite is opposite the angle

Sine, cosine, and tangent

The three main functions in trigonometry are Sine, Cosine and Tangent.

They are just the length of one side divided by another

For a right triangle with an angle θ :

Sine Function:	sin(θ) = Opposite / Hypotenuse
Cosine Function:	cos(θ) = Adjacent / Hypotenuse
Tangent Function:	tan(θ) = Opposite / Adjacent

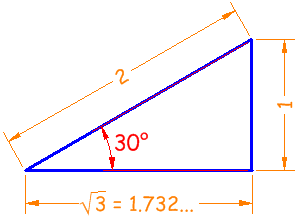
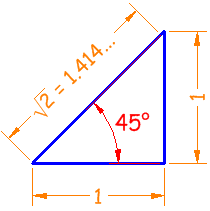
For a given angle θ each ratio stays the same
no matter how big or small the triangle is

When we divide Sine by Cosine we get:

So we can say:

tan(θ) = sin(θ)/cos(θ)

That is our first Trigonometric Identity.

Cosecant, secant, and cotangent

We can also divide "the other way around" (such as Adjacent/Opposite instead of Opposite/Adjacent):

	csc(θ) = Hypotenuse / Opposite
	sec(θ) = Hypotenuse / Adjacent
	cot(θ) = Adjacent / Opposite

Example: when Opposite = 2 and Hypotenuse = 4 then

sin(θ) = 2/4, and csc(θ) = 4/2

Because of all that we can say:

sin(θ) = 1/csc(θ)

cos(θ) = 1/sec(θ)

tan(θ) = 1/cot(θ)

And the other way around:

csc(θ) = 1/sin(θ)

sec(θ) = 1/cos(θ)

cot(θ) = 1/tan(θ)

And we also have:

cot(θ) = cos(θ)/sin(θ)

Sohcahtoa

How to remember? Think "Sohcahtoa"!

It works like this:

Soh...	Sine = Opposite / Hypotenuse
...cah...	Cosine = Adjacent / Hypotenuse
...toa	Tangent = Opposite / Adjacent

You can read more about sohcahtoa please remember it, it may help in an exam ! 

Examples

Example: what are the sine, cosine and tangent of 30° ?

The classic 30° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of √3:

Now we know the lengths, we can calculate the functions:

Sine		sin(30°) = 1 / 2 = 0.5
Cosine		cos(30°) = 1.732 / 2 = 0.866...
Tangent		tan(30°) = 1 / 1.732 = 0.577...

(get your calculator out and check them!)

Example: what are the sine, cosine and tangent of 45° ?

The classic 45° triangle has two sides of 1 and a hypotenuse of √2:

Sine		sin(45°) = 1 / 1.414 = 0.707...
Cosine		cos(45°) = 1 / 1.414 = 0.707...
Tangent		tan(45°) = 1 / 1 = 1

Why?

Why are these functions important?

• Because they let us work out angles when we know sides
• And they let us work out sides when we know angles

Example: Use the sine function to find "d"

We know:

• The cable makes a 39° angle with the seabed
• The cable has a 30 meter length.

And we want to know "d" (the distance down).

Start with:		sin 39° = opposite/hypotenuse
		sin 39° = d/30
Swap Sides:		d/30 = sin 39°
Use a calculator to find sin 39°:		d/30 = 0.6293…
Multiply both sides by 30:		d = 0.6293… x 30
		d = 18.88 to 2 decimal places.

The depth "d" is 18.88 m