Trigonometry

Trigonometry ... is all about triangles.

Normally we using right-angled triangle to represent the triangles.

• Adjacent: adjacent (next to) the angle θ
• Opposite: opposite the angle θ
• and the longest side is the Hypotenuse

Why is this triangle so important?
Imagine we can measure along and up but want to know the direct distance and angle:

Or we have a distance and angle and need to "plot the dot" along and up:

Questions like these are common in engineering, computer animation and more.
And trigonometry gives the answers!

Sine, Cosine and Tangent

They are simply one side of a right-angled triangle divided by another.

For any angle "θ":

(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.)

Example: What is the sine of 35°?

Using this triangle (lengths are only to one decimal place):

sin(35°) = OppositeHypotenuse = 2.84.9 = 0.57...

Calculators have sin, cos and tan, let's see how to use them:

Example: What is the missing height here?

• We know the Hypotenuse
• We want to know the Opposite

Sine is the ratio of Opposite / Hypotenuse:

sin(45°) = OppositeHypotenuse

Get a calculator, type in "45", then the "sin" key:

sin(45°) = 0.7071...

0.7071... is the ratio of the side lengths: in other words the Opposite is about 0.7071 times as long as the Hypotenuse.
Maybe you can figure out the height now?
But let's do it formally using some algebra:

Start with:sin(45°) = OppositeHypotenuse

Put in what we know:0.7071... = Opposite20

Swap sides:Opposite20 = 0.7071...

Multiply both sides by 20:Opposite = 0.7071... × 20

Calculate:Opposite = 14.14 (to 2 decimals)

Done!

Try Sin, Cos and Tan

Play with this for a while (move the mouse around) and get familiar with values of sine, cosine and tangent for different angles, such as 0°, 30°, 45°, 60° and 90°.

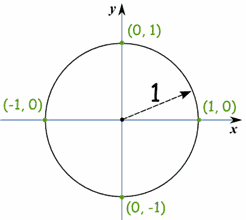
Unit Circle

• What you just played with is the unit circle.
• It is a circle with a radius of 1 with its center at 0.
• Because the radius is 1, we can directly measure sine, cosine and tangent.

Here we see the sine function being made by the unit circle:

And now you know why trigonometry is also about circles!

(Note: you can see the nice graphs made by sine, cosine and tangent.)

Degrees and Radians

Angles can be in Degrees or Radians. Here are some examples:

Angle	Degrees	Radians
Right Angle	90°	π/2
__ Straight Angle	180°	π
Full Rotation	360°	2π

Repeating Pattern

The angle is rotating around and around the circle the Sine, Cosine and Tangent functions repeat once every full rotation.

When we want to calculate the function for an angle larger than a full rotation of 360° (2π radians) we subtract as many full rotations as needed to bring it back below 360° (2π radians):

Example: what is the cosine of 370°?

370° is greater than 360° so let us subtract 360°

370° − 360° = 10°

cos(370°) = cos(10°) = 0.985 (to 3 decimal places)

And when the angle is less than zero, just add full rotations.

Example: what is the sine of −3 radians?

−3 is less than 0 so let us add 2π radians

−3 + 2π = −3 + 6.283... = 3.283... radians

sin(−3) = sin(3.283...) = −0.141 (to 3 decimal places)

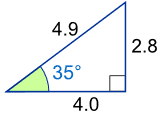
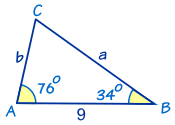
Solving Triangles

A big part of Trigonometry is solving problem. "Solving" means finding missing sides and angles.

Example: Find the Missing Angle "C"

Angle C can be found using angles of a triangle add to 180°:

So C = 180° − 76° − 34° = 70°

We can also find missing side lengths. The general rule is:

When we know any 3 of the sides or angles we can find the other 3

(except for the three angles case)

Other Functions (Cotangent, Secant, Cosecant)

Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:

Cosecant Function:	csc(θ) = Hypotenuse / Opposite
Secant Function:	sec(θ) = Hypotenuse / Adjacent
Cotangent Function:	cot(θ) = Adjacent / Opposite

Trigonometric and Triangle Identities

And as you get better at Trigonometry you can learn:

• The trigonometric identities are equations that are true for all right-angled triangles.
• The triangle identities are equations that are true for all triangles (note: they don't have a right angle).