Algebra

Basic Algebra normally contain three simple basic category which are:

1. Adding and Subtracting of Algebraic Expressions
2. Multiplication of Algebraic Expressions
3. Division of Algebraic Expressions

Adding and Subtracting Terms

EXAMPLE:

Simplify 13x + 7y − 2x + 6a

13x + 7y − 2x + 6a
The only like terms in this expression are $\displaystyle{13}{x}$ and $\displaystyle-{2}{x}$. We cannot do anything with the $\displaystyle{7}{y}$ or $\displaystyle{6}{a}$.
So we group together the terms we can subtract, and just leave the rest:

(13x − 2x) + 6a + 7y
= 6a + 11x + 7y

We usually present our variables in alphabetical order, but it is not essential.

Important note: We can only add or subtract like terms.

Why? Think of it like this. 

• On a table we have 4 pencils and 2 books. 
• We cannot add the 4 pencils to the 2 books because they are not the same kind of object.
• While, we go get another 3 pencils and 6 books.
• Altogether we now have 7 pencils and 8 books. 
• We can't combine these quantities, since they are different types of objects.

Similarly with algebra, we can only add (or subtract) similar "objects", or those with the same letter raised to the same power.

Multiplication of Algebraic Expressions

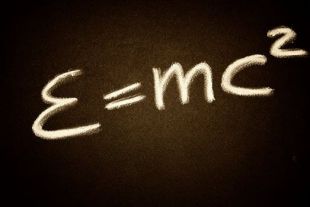
Einstein's famous equation involves multiplying algebraic terms

When we multiply algebraic expressions, we need to remember the index law from the Numbers chapter.

Let's see how algebra multiplication works with a series of examples.

EXAMPLE 1:

Multiply (x + 5)(a − 6)

We multiply this out as follows. We take each term of the first bracket and multiply them by the second bracket. Then we expand out the result.

(x + 5)(a − 6)
= x(a − 6) + 5(a − 6)
= ax − 6x + 5a − 30

We cannot do any more with this answer. There are no like terms, so we cannot simplify it in any way.

EXAMPLE 2:

Multiply $\displaystyle{\left({x}-{3}\right)}^{2}$

= (x − 3)(x − 3)
= x(x − 3) − 3(x − 3)
= x² − 3x − 3x + 9
= x² − 6x + 9

Important Note:

$\displaystyle{\left({x}-{3}\right)}^{2}$

                                                 is NOT equal to

$\displaystyle{x}^{2}-{9}$

Please take note of this! Many students confuse this idea and it's not surprising because sometimes the way we write math is not consistent.

Division of Algebraic Expressions

EXAMPLE:

Simplify $\displaystyle\frac{{{3}{a}{b}{\left({4}{a}^{2}{b}^{5}\right)}}}{{{8}{a}^{2}{b}^{3}}}$

First, we multiply out the top line:

$\displaystyle\frac{{{12}{a}^{3}{b}^{6}}}{{{8}{a}^{2}{b}^{3}}}$

When we write it out in full, this means

$\displaystyle\frac{{{12}\times{a}{a}{a}\times{b}{b}{b}{b}{b}{b}}}{{{8}\times{a}{a}\times{b}{b}{b}}}$

Next, cancel the numbers top and bottom (we divide top and bottom by $\displaystyle{4}$), the "a" terms (we cancel $\displaystyle{a}^{2}={a}{a}$ from top and bottom) and the "b" terms (we cancel $\displaystyle{b}^{3}={b}{b}{b}$ from top and bottom) to give us the final answer:

$\displaystyle\frac{{{3}{a}{b}^{3}}}{{2}}$