Sine, Cosine and Tangent in the Four Quadrants

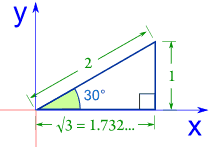
Now let us look at what happens when we place a 30° triangle in each of the 4 Quadrants.

In Quadrant I everything is normal, and Sine, Cosine and Tangent are all positive:

Example: The sine, cosine and tangent of 30°

Sine	sin(30°) = 1 / 2 = 0.5
Cosine	cos(30°) = 1.732 / 2 = 0.866
Tangent	tan(30°) = 1 / 1.732 = 0.577

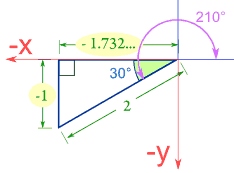
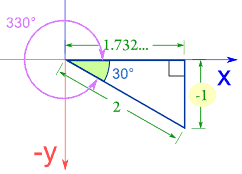
But in Quadrant II, the x direction is negative, and both cosine and tangent become negative:

Example: The sine, cosine and tangent of 150°

Sine	sin(150°) = 1 / 2 = 0.5
Cosine	cos(150°) = −1.732 / 2 = −0.866
Tangent	tan(150°) = 1 / −1.732 = −0.577

In Quadrant III, sine and cosine are negative:

Example: The sine, cosine and tangent of 210°

Sine	sin(210°) = −1 / 2 = −0.5
Cosine	cos(210°) = −1.732 / 2 = −0.866
Tangent	tan(210°) = −1 / −1.732 = 0.577

Note: Tangent is positive because dividing a negative by a negative gives a positive.

In Quadrant IV, sine and tangent are negative:

Example: The sine, cosine and tangent of 330°

Sine	sin(330°) = −1 / 2 = −0.5
Cosine	cos(330°) = 1.732 / 2 = 0.866
Tangent	tan(330°) = −1 / 1.732 = −0.577

There is a pattern! Look at when Sine Cosine and Tangent are positive ...

• All three of them are positive in Quadrant I
• Sine only is positive in Quadrant II
• Tangent only is positive in Quadrant III
• Cosine only is positive in Quadrant IV

This can be shown even easier by:

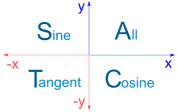
Some people like to remember the four letters ASTC by one of these: All Students Take Chemistry All Students Take Calculus All Silly Tom Cats All Stations To Central Add Sugar To Coffee You can remember one of these, or maybe you could make up your own. Or just remember ASTC.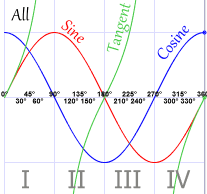

This graph shows "ASTC" also.